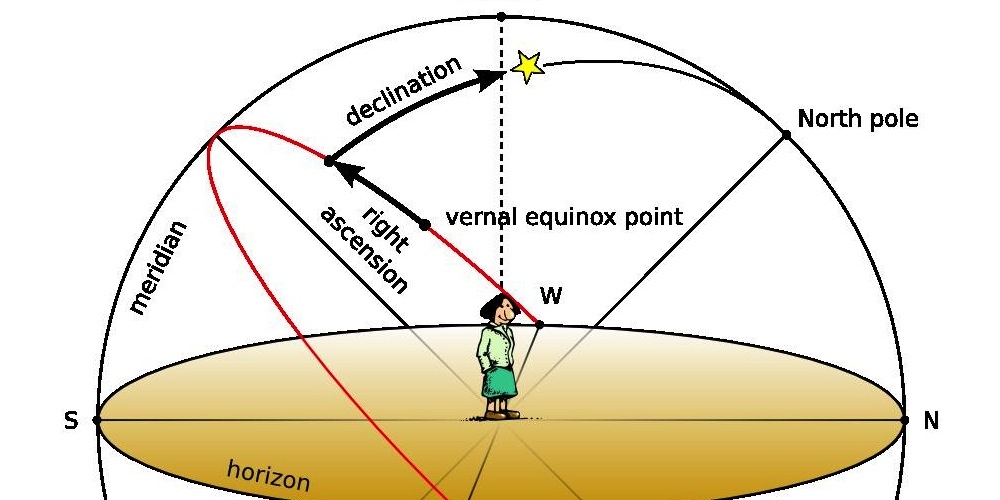
Om de posities van hemelobjecten vast te leggen, gebruikte men jaren het systeem van hoogte en azimut. Hierbij deed zich wel het probleem voor dat de hemelbol voortdurend in beweging is, en deze coördinaten bijgevolg voortdurend veranderen. Daarom was men genoodzaakt een nieuw coördinatenstelsel aan de hemelbol toe te voegen: het coördinatensysteem van declinatie en rechte klimming, wat zeer belangrijk is voor de moderne astronoom.
Hoogte en azimut
De hoogte van een hemelobject aan de hemel wordt gemeten en onderverdeeld in 90 booggraden tussen de horizon en het zenit (het punt recht boven het hoofd van de waarnemer). Belangrijk hierbij is om te weten dat één booggraad 60 boogminuten bevat, en één boogminuut op zijn beurt 60 boogseconden bevat. Het azimut daarentegen geeft aan in welke kompasrichting een hemelobject is gelegen. De volledige azimutcirkel bedraagt exact 360°. Zo krijgt een hemelobject dat precies in het noorden is gelegen een azimut van 0°, een object in het oosten een azimut van 90°, een object in het zuiden een azimut van 180°, ... Samen met de hoogte vormt het azimut het azimutaal coördinatensysteem en is bijvoorbeeld handig om weer te geven waar een satelliet zal verschijnen (bijvoorbeeld hoogte 56° en azimut 140°).
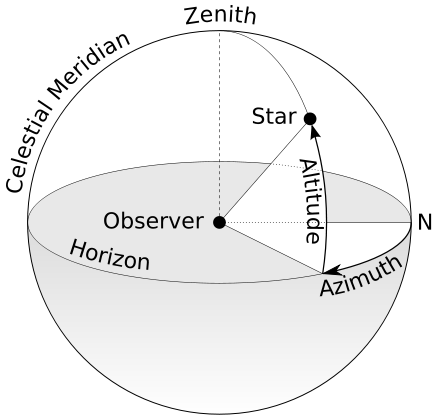
Foto: TWCarlson
Declinatie en rechte klimming
Ten gevolge van de aardrotatie is de sterrenhemel voortdurend in beweging, en dus werd de nood aan een coördinatenstelsel waarbij de coördinaten van een object ongewijzigd blijven, ongeacht datum, tijdstip en plaats, steeds groter. Daarom werd het systeem van declinatie en rechte klimming ingevoerd. De declinatie van een hemelobject wordt net zoals de hoogte gemeten in graden, met als groot verschil dat de declinatie de positie van een object aangeeft ten opzichte van de hemelequator (projectie van de aardevenaar op de hemelbol), en wordt gemeten van -90 tot 90° (van zuidelijke hemelpool tot noordelijke hemelpool). Een hemelobject dat zich boven de hemelequator (of hemelevenaar) bevindt, krijgt een positieve declinatie toegekend, terwijl een hemelobject dat zich onder de hemelevenaar bevindt een negatieve declinatie krijgt. Een object dat zich precies op de hemelequator bevindt krijgt als declinatie 0°.
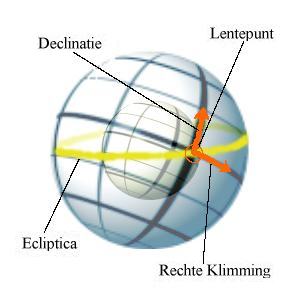
Foto: Ulrich.fuchs and BenTels
Het systeem van rechte klimming kan vergeleken worden met het azimut. Deze wordt echter niet in booggraden gemeten, maar in uren, die opgedeeld kunnen worden in minuten en seconden. Samen met de declinatie vormt de rechte klimming het systeem van de equatoriale coördinaten, en wordt gemeten vanaf het Lentepunt of Punt Ram. In tegenstelling tot wat de naam doet vermoeden, is het Punt Ram niet gelegen in het sterrenbeeld Ram. Dit is een resultante van de precessie, de tolbeweging van de aarde waardoor de hemelpool in zeer lange tijd een cirkelvormige beweging beschrijft, en hierdoor is het Lentepunt nu gelegen in het naburige sterrenbeeld Pisces (Vissen).
De culminatie van een hemelobject
Elk hemelobject zal, na verloop van tijd, een maximale hoogte aan de hemel bereiken. In de sterrenkunde staat dit moment bekend als de culminatie, een begrip ingevoerd door Sir Isaac Newton. De culminatie zal altijd plaatsvinden op de cirkel die door het noorden gaat, onderweg het zenit kruist, en vervolgens door het zuiden en het nadir (punt recht tegenover het zenit, heeft als hoogte -90°) gaat. Om te berekenen op welke hoogte de culminatie zal plaatsvinden kan men gebruik maken van volgendeeenvoudige formule, waarin de breedteligging een belangrijke rol speelt, want als men bijvoorbeeld één geografische graad daalt in breedte (bijv. van 51°NB naar 50°NB), dan daalt eenzelfde hemelobject ook 1° aan de hemel;
90° - geografische breedte waarnemer + declinatie hemelobject = hoogte culminatie
Bijvoorbeeld, om de hoogte van de culminatie van de ster Bèta Orionis (Rigel) te bepalen, wanneer men zich bevindt op 35°ZB:
Gegeven:
- Breedtegraad: 51°ZB (in formule GEEN -35° gebruiken)
- Declinatie object: −8° 12' 6''
hoogte culminatie = 90° - 51° + (-8°12'6'')
⇕
hoogte culminatie = 90° - 51° - 8°12'6''
⇕
hoogte culminatie = 30°48'54''
Merk bij deze formule ook op dat wanneer men deze invult voor de hemelequator, de declinatie gelijk is aan het verschil van 90° met de geografische breedteligging. Soms kan het ook interessant zijn om te weten hoeveel graden een hemelobject onder de horizon culmineert, zo geldt op 50°NB voor de ster Epsilon Indi:
Gegeven:
- Breedtegraad: 50°NB
- Declinatie object: -56° 47' 10"
hoogte culminatie = 90° - 50° + (-56°47'10")
⇕
hoogte culminatie = 90° - 50° - 56°47'10''
⇕
hoogte culminatie = -13°13'50''
Hieruit kunnen we besluiten dat de ster Epsilon Indi op 50°NB 13°13'50'' onder de horizon culmineert.